INSTITUCIÓN EDUCATIVA ALFREDO BONILLA MONTAÑO
MATEMÁTICAS PRIMER PERIODO GRADO 7
Tema: Multiplicación y División de números Enteros
Licenciada DIXI
SUAREZ B.
Ideas Previas
1- Expresa las siguientes multiplicaciones como una suma de sumandos iguales.
a. 2 x 7 b. 9 x 3 c. 4 x 125
2- Halla el resultado en cada caso.
a. (-2) + (-2) + (-2) + (-2) + (-2)
b. (-6) + (-6) +(-6)
El banco donde Sofía tiene su cuenta de ahorros le cobre $1.100 cada vez que ella realiza una transacción con su tarjeta débito en un cajero automático de la red a la que pertenece el banco. Esta mes, Sofia 7 transacciones bancarias: 3 consignaciones de $100.000 cada una y 4 consultas de saldo en cajeros de la red usando su tarjeta débito.
Si calculamos el valor de las transacciones concluimos que Sofìa consignó $300.000 y el banco le descontó $4.400 por usar la tarjeta. Así:
Dinero consignado: 3 x 100.00 = 300.000
Dinero descontado: 4 x (-1.100) = (-1.100) + (-1.100) + (-1.100) + (-1.100) = - 4.400
Escribimos -1.100 para indicar que ese dinero se debitó a su cuenta.
Para multiplicar dos números enteros se multiplican sus valores absolutos. Si los números tienen igual signo, el resultado es positivo; si tienen signos diferentes, el resultado es negativo.
Ejemplo 1
Calculemos los productos indicados.
a. (-3) x (-7) b. 3 x 7 c. (-3) x 7 d. 3 x (-7)
Solución:
Como | -3| = 3 y |-7| = 7 hallamos el producto 3 x 7 = 21 y determinamos el signo de cada producto así
a. (-3) x (-7) = 21 Los factores tienen igual signo, entonces, el producto es positivo
b. 3 x 7 = 21 Los factores tienen igual signo, entonces, el producto es positivo
c. (-3) x 7 = -21 Los factores tienen signos diferentes, entonces, el producto es negativo
d. 3 x (-7) = -21 Los factores tienen signos diferentes, entonces, el producto es negativo
Ejemplo 2
Si x = -3, z = -4 y w = 2, evaluemos las siguientes expresiones.
a. (x - z) X w
b. (x X w) + z
Solución:
a. (x - z) X w = ((-3) - (-4)) X 2 = ( -3 + 4) X 2 = 1 X 2 = 2
b. (x X w) + z = (-3 x 2) + (-4) = (-6) + (-4) = -10
Tarea: Consulta las propiedades de la multiplicación de número enteros copiarlas
y realiza un ejemplo de cada una.
División de Números Enteros: Para
dividir dos número enteros, se dividen sus valores absolutos. Si los números tienen
igual signo, el resultado es
positivo; si tienen
signos diferentes, el resultado es
negativo.
El cociente de dos números enteros no es siempre un número entero. Por ejemplo 7/5 = 1,4. En este tema solo estudiaremos la división exacta de números enteros.
Ejemplo 3
Efectuemos las siguientes operaciones:
a. (-21) / (-7)
b. (45/5) - (35/-7)
Solución:
a. (-21) / (-7) = 3. El cociente de dos números enteros con el mismo signo es
positivo.
b. (45/5) - (35/ -7) = 9 - (-5) = 9 + 5 = 14. Realizamos primero las divisiones de lo que está dentro de los paréntesis y finalmente la sustracción.
DESARROLLA COMPETENCIAS
1. Efectúa las operaciones indicadas.
a. ((-2) + 5 + (-7)) x ( 8 - 6 -1)
b. (-15 / 5) + (-15)
c. (-45/9) x (49 / 7)
d. (-9 x 3) - (64 / 8)
2. Efectúa las multiplicaciones.
a- (-13) x 5
b- 42 x 16
c- (-11) x (-8) x 4
d. 15 x (-2) x 10
3. Explica sin realizar la operación cómo se puede saber si el cociente de cada división es un entero.
a. -3758 / -2
b. 8931 / -3
c. -37190 / 5
d. -5832 / 6
*Se recomienda recordar los criterios de divisibilidad
4. Efectúa las siguientes divisiones.
a. -81 / 27
b. -36 / -4
c. 8178 / 94
d. (-36 / 4) / 3
5. Halla lo que se solicita en cada caso.
a. El opuesto del resultado de (63 / -9) x (-4 -6)
b. El cociente del valor absoluto de -69 y el opuesto de 23
c. El producto del opuesto de -7 y el opuesto de 15
Razonamiento lógico.
6. Escribe en el espacio el número entero que corresponde y la propiedad que aplicas.
a. (___ x 6) x -3 = -2 x ( 6 x ___)
b. ___ x -39 = -39 x ___ = -39
c. (-3 + 5) x 7 = ___ x (-3 + 5) =
d. 4 x (6 + (-5)) = 4 x ___ + 4 x ___
e. ___ x (-5 x -2) = -5 x 2
7. Determina si cada afirmación es verdadera o falsa. Justifica tu respuesta.
a. El producto de dos números enteros es mayor que cada factor.
b. La división de dos números enteros siempre da como resultado un número entero.
c. Uno es el único número entero que divide exactamente a todos los números enteros.
d. Si un número es producto de dos enteros, también es producto de sus opuestos.
Pensamiento crítico y resolución de problemas
8. Encuentra los números enteros que satisfacen las condiciones dadas.
a. Suma: -18; cociente: 8
b. Suma: 4; producto: -12
c. Diferencia: 10; producto: -16
d. Diferencia: -14; cociente: -6
9. Cecilia recibió 9 cheques de $250.000 cada uno. Cuando intentó cambiarlos en el banco, solamente 5 se hicieron efectivo y los otros 4 fueron rechazados. ¿Cuánto dinero recibió Cecilia? ¿Cuánto dinero le faltó por cobrar?
10. Un buzo debe atar unos banderines a una cuerda para indicar la profundidad a la que se encuentra. Si estos banderines deben ir situados cada 7 metros. ¿Cuántos ha puesto cuando se encuentra a -175 metros?
Dios les bendiga.






![\sqrt[n]{b}=a \sqrt[n]{b}=a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b2480dff4dea5bb8f396c9367ebbdbac.gif)
![\sqrt[4]{256}=4 \sqrt[4]{256}=4](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/2e642668f3c78782d542932a35966a93.gif)

![\sqrt[3]{125}=5 \sqrt[3]{125}=5](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e36c9a48d939b17b33dbd676c6b7713c.gif)
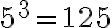
![\sqrt[6]{64}=2 \sqrt[6]{64}=2](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/40c3716007528d6dfdcc641bb4483161.gif)