INSTITUCIÓN EDUCATIVA ALFREDO BONILLA MONTAÑO
GEOMETRÍA, SEGUNDO SEMESTRE GRADO 7
Tema: PERÍMETRO DE LA CIRCUNFERENCIA Y ÁREA DEL CÍRCULO
Licenciada: DIXI SUAREZ B.
IDEAS PREVIAS:
1- Imagina que estás hablando por teléfono con un amigo y necesitas darle la definición de circunferencia, qué le dirás?
2- Qué diferencia hay entre el Círculo y la Circunferencia?
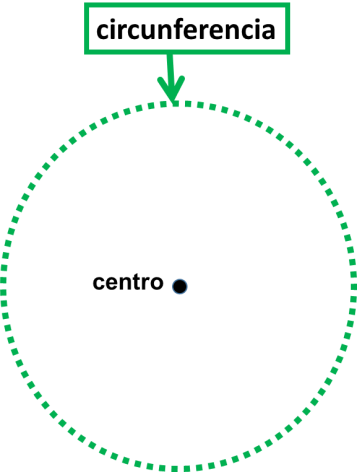
La circunferencia es el conjunto de puntos que se encuentran a una misma distancia de otro llamado centro.
El perímetro de la circunferencia es la medida de su longitud. Se puede obtener de dos maneras:
1).- Multiplicando “pi” (π) por diámetro
P = π x d
2).- Multiplicando dos veces “pi” por el radio
P = 2π x r
Cuando nos referimos al perímetro hablamos de unidades simples, ya que se mide sólo una dimensión: la longitud.
Veamos un ejemplo.
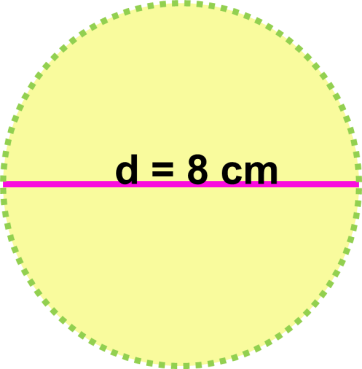
Obtener el perímetro de la circunferencia del siguiente círculo (la longitud de la línea verde punteada).
Con la primera fórmula:
P = π x d
P = 3.1416 X 8
P = 25.1328 cm
Con la segunda fórmula (recuerda que el radio es igual a la mitad del diámetro).
P = 2π x r
P = 2(3.1416) x 4
P = 6.2832 x 4
P = 25.1328 cm
SEGMENTOS NOTABLES
Diámetro: Es el segmento que une dos puntos de la circunferencia pasando por el centro.
Radio: Es el segmento que une el centro con cualquier punto de la circunferencia. Es la mitad de diámetro.
Arco: Es una parte de la circunferencia que se delimita entre dos puntos.
Cuerda: Es el segmento que une dos puntos de la circunferencia.
El círculo es la superficie que queda limitada por la circunferencia.
El área del círculo es la medida de su superficie, como se trata de dos dimensiones, el resultado se da siempre en unidades cuadráticas o cuadradas.
El área del círculo se obtiene con la fórmula: pi por radio al cuadrado.
A = π x r²
Obtener el área del siguiente círculo (la superficie amarilla).
A = π x r²
A = 3.1416 x 4²
A = 3.1416 x 16
A = 50.2656 cm²






No hay comentarios:
Publicar un comentario